Equipotential lines are a way to represent that the electric potential will be the same everywhere along that line. In other words, if we take a voltmeter and start to make measurements along the equipotential line, all the values will be the same (or will differ by very small values since we don’t live in a perfect world)

Since the electric potential is the same all across some equipotential (\(\Delta V=0\)), moving a charge across it requires no work whatsoever. Also, these equipotential lines are perpendicular to the electric field vectors meaning we can give an numeric proof that \(W=0\)
\[W=q|\overrightarrow{E}|r\cos\pi=0\]Visualizing the equipotential
The formula to obtain the electric potential is:
\[V=\frac{kQ}{r}\]We can use this value as a sort of \(z\) axis for the vector plot of the previous post, other way of seeing it is by imagining this value V will be the weight of that vector, the further away from the charge, the lighter it is. For this we need to add a new global variable \(V\) and add some code to the function that creates point charges. This will create the matrix of values for the z axis.
V = V + k.*q./(sqrt(Cx.^2 + Cy.^2));
After that, using the contour function we can plot these values as lines that will have a color depending on their weight.
hold on
contour(xS,yS, V, line_amount);
These are the results with 300 lines of density
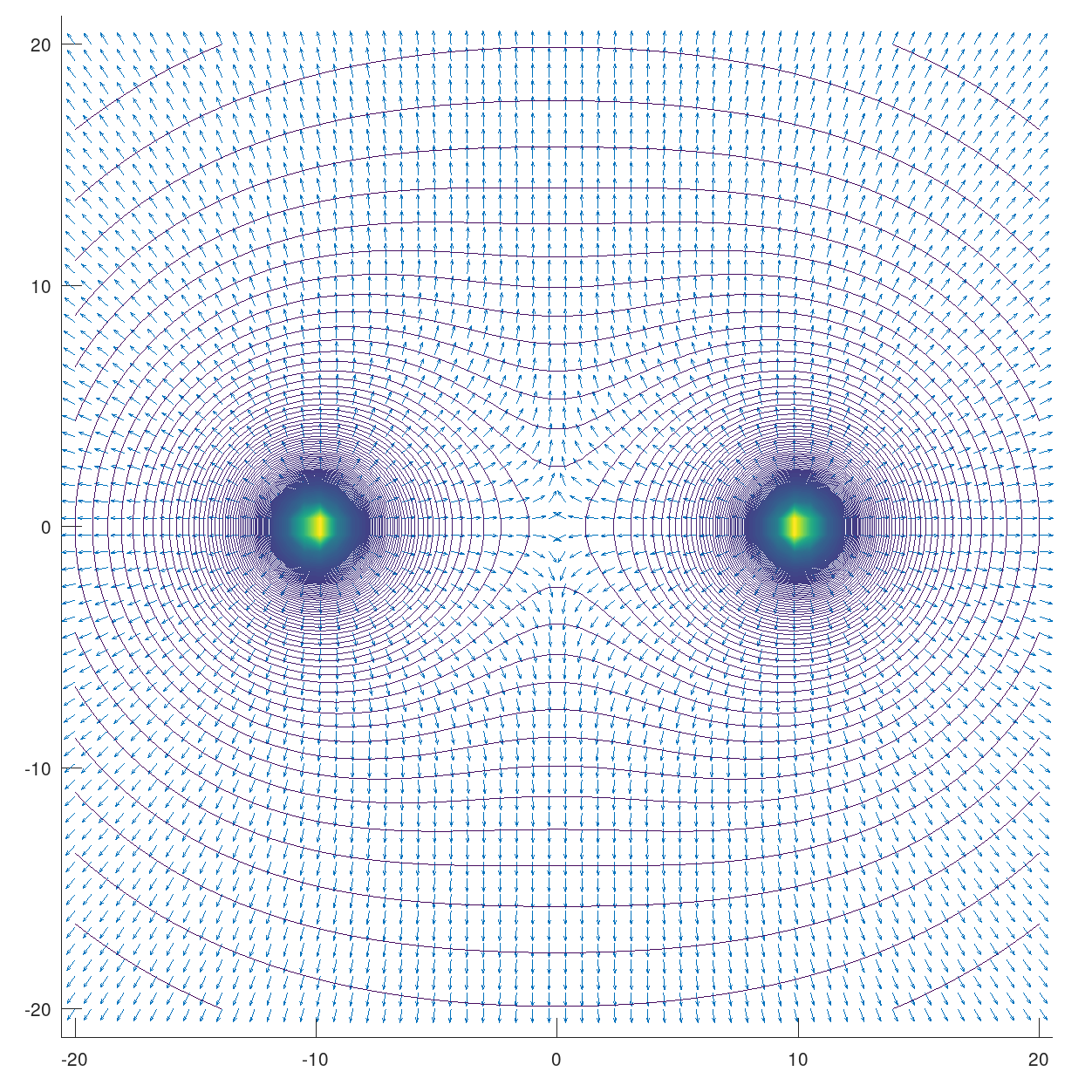
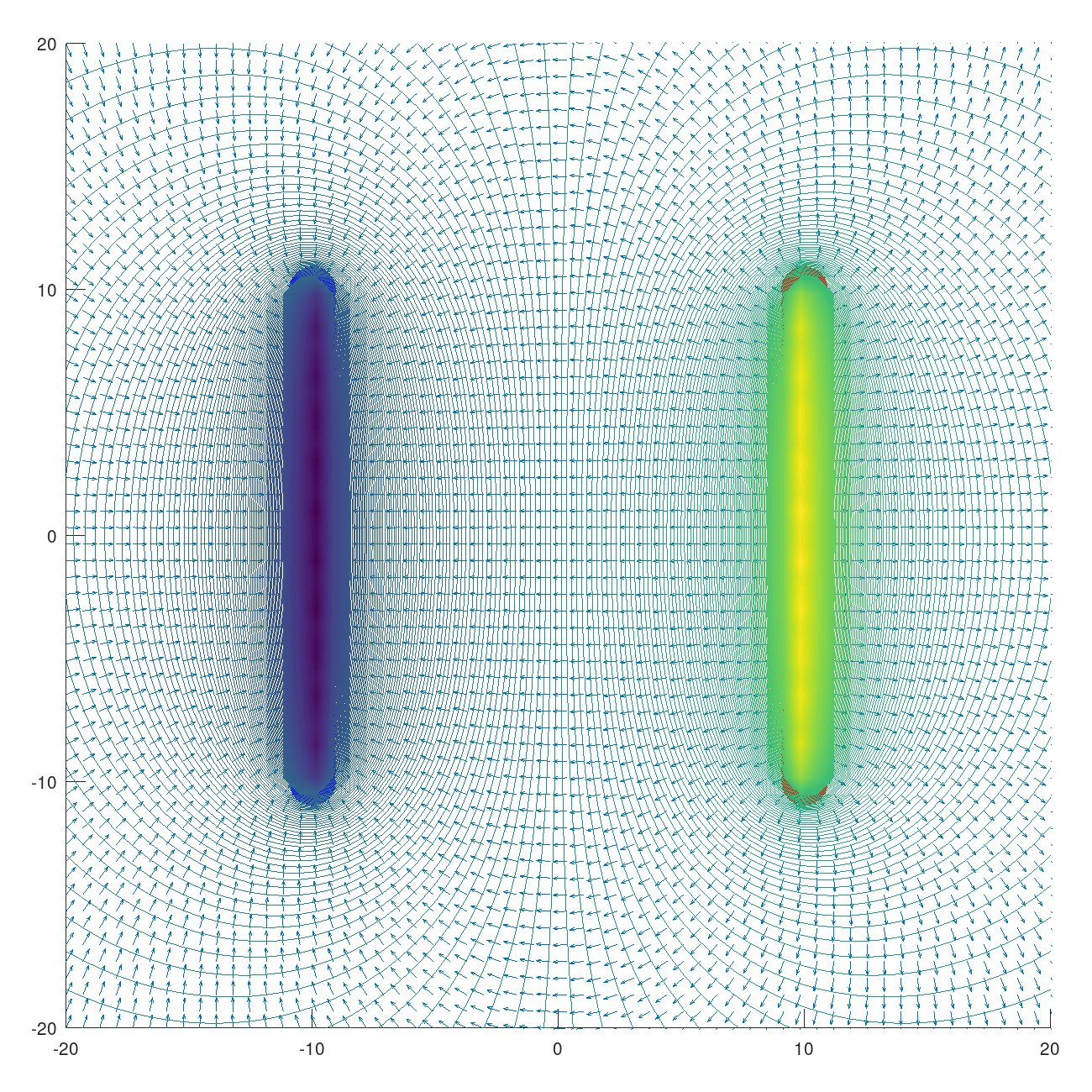

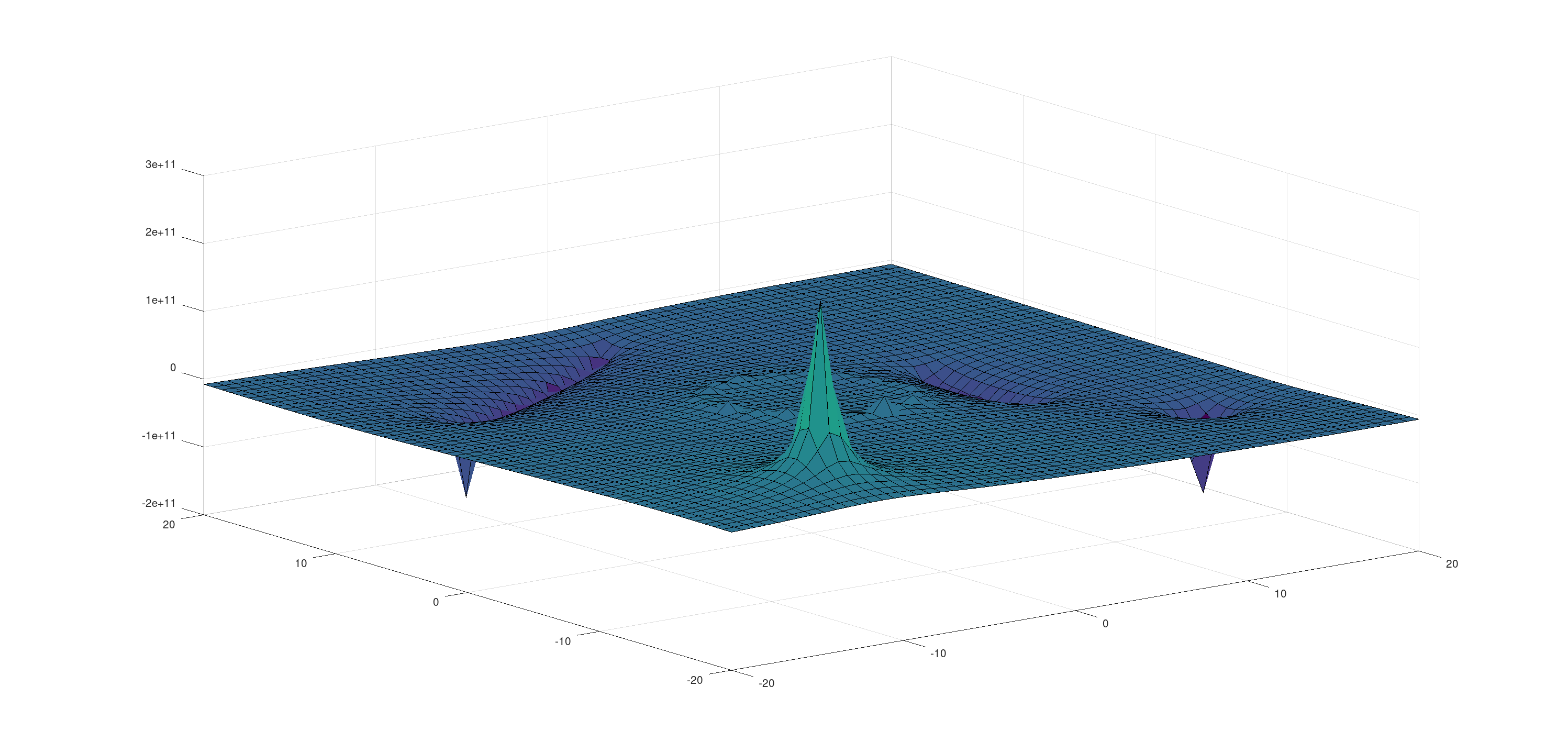
If we do a surface plot of this \(V\) matrix, we get something similar to those gravity force plots that we see solar system videos :P
An experiment you can try
Using the same setup as the previous post, change the oil for water and try to simulate the shapes you want to recreate, then print that graphic and put it on your tray while trying to align the center of your shapes with the ones in the graphic. Then take your voltmeter and verify if the measurements along different equipotential lines has little to no difference.
Here is all the code so far to visualize electric fields in GNU Octave (this should work in Matlab too)
clear; close all; clc;
%grid
N=60; %density
Vd=300; %equipotential lines
minX=-20;maxX=+20; %grid size
minY=-20;maxY=+20;
xl=linspace(minX,maxX,N); %evenly spaced N vectors per row
yl=linspace(minY,maxY,N);
global xS;
global yS;
global Ex;
global Ey;
global V;
[xS,yS]=meshgrid(xl,yl); %vector grid
%electric field components
Ex=0;
Ey=0;
V=0;
%q=charge x,y=position in the grid
function efield = place_charge(q,x,y)
global xS;
global yS;
global Ex;
global Ey;
global V;
%constants
eps0 = 8.854e-12;
k = 1/(4*pi*eps0);
%vector coordinates in the spaces where the point charge is placed
Cx = xS-x;
Cy = yS-y;
C = sqrt(Cx.^2 + Cy.^2).^3;
%electric field calculation
Ex = Ex + k .* q .* Cx ./ C;
Ey = Ey + k .* q .* Cy ./ C;
%electric potential calculation
V = V + k.*q./(sqrt(Cx.^2 + Cy.^2));
hold on;
if(q<0)
plot(x, y, 'b', 'MarkerSize', 80);
else
plot(x, y, 'r', 'MarkerSize', 80);
end
end
function linefi = place_line(q,x0,y0,x1,y1)
lambda = q ./ sqrt( (x1-x0).^2 + (y1-y0).^2);
step=abs(lambda);
dx=x1 - x0;
dy=y1 - y0;
m=dy ./ dx;
b=y0 - m .* x0;
if x1==x0
%Do sweep across y axis
if(y0>y1)
step*=-1;
endif
for i = y0:step:y1
place_charge(lambda,x0,i);
end
else
%Do sweep across x axis
if(x0>x1)
step*=-1;
endif
for i = x0:step:x1
place_charge(lambda,i,m.*i + b); %y = mx+b
end
end
end
function ringfi = place_ring(q,x,y,r)
lambda = q ./ (6.28318530717958647693.*r);
step=abs(lambda);
for i=0:step:6.28318530717958647693
place_charge(lambda,x+r*cos(i),y+r*sin(i));
endfor
end
%shapes
place_ring(10,0,0,5);
place_line(-10,10,4,10,-4);
place_charge(-5,15,-10);
place_line(-10,1,17,-14,9);
place_charge(10,-11,-15);
%shapes
%normalize transforms
E = sqrt(Ex.^2 + Ey.^2);
u = Ex./E;
v = Ey./E;
%plot electric field
quiver(xS,yS,u,v,'autoscalefactor',0.6);
hold on
%plot equipotential
contour(xS,yS, V,Vd);
axis([-20 20 -20 20]);
axis equal;
%3d plot
figure();
surf(xS,yS,V);